数据结构&排序算法

深度优先(DFS)

深度优先搜索英文缩写为 DFS 即Depth First Search
其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次
应用场景
- React 虚拟 DOM 的构建
- React 的 fiber 树构建

实现思路

先访问根节点，如果有children，遍历children节点，递归dfs

// 对象的情况
function dfs(node) {
  console.log(node.name);
  node.children &&
    node.children.forEach((child) => {
      dfs(child);
    });
}
let root = {
  name: "A",
  children: [
    {
      name: "B",
      children: [{ name: "B1" }, { name: "B2" }],
    },
    {
      name: "C",
      children: [{ name: "C1" }, { name: "C2" }],
    },
  ],
};
dfs(root); // A B B1 B2 C C1 C2

// 数组的情况
function dfs(root){
  root && root.forEach(node => {
    console.log(node.name);
    dfs(node.children)
  });
}
let root = [
  {
    name: "A",
    children: [
      {
        name: "B",
        children: [{ name: "B1" }, { name: "B2" }],
      },
      {
        name: "C",
        children: [{ name: "C1" }, { name: "C2" }],
      },
    ],
  },
  {
    name: "A1",
    children: [
      {
        name: "B1",
        children: [{ name: "B11" }, { name: "B21" }],
      },
      {
        name: "C1",
        children: [{ name: "C11" }, { name: "C21" }],
      },
    ],
  },
];
dfs(root)

广度优先(BFS)

宽度优先搜索算法（又称广度优先搜索），其英文全称是 Breadth First Search
算法首先搜索距离为k的所有顶点，然后再去搜索距离为k+l的其他顶点

实现思路(利用栈的特性)

1、首先创建一个数组，将根节点添加到数组中
2、进入while循环，每次取栈顶的节点，如果节点中有children，遍历children节点，添加到数组中

// 对象的情况
function bfs(node) {
  const stack = [];
  stack.push(node);
  let current = stack.shift()
  while (current) {
    console.log(current.name);
    current.children &&
      current.children.forEach((child) => {
        stack.push(child);
      });
      current = stack.shift()
  }
}
let root = {
  name: "A",
  children: [
    {
      name: "B",
      children: [{ name: "B1" }, { name: "B2" }],
    },
    {
      name: "C",
      children: [{ name: "C1" }, { name: "C2" }],
    },
  ],
};
bfs(root); // A B C B1 B2 C1 C2

// 数组的情况
function bfs(root){
  root && root.forEach(node => {
    const stack = [];
    stack.push(node);
    let current = stack.shift()
    while (current) {
      console.log(current.name);
      current.children &&
        current.children.forEach((child) => {
          stack.push(child);
        });
        current = stack.shift()
    }
  });
}

let root = [
  {
    name: "A",
    children: [
      {
        name: "B",
        children: [{ name: "B1" }, { name: "B2" }],
      },
      {
        name: "C",
        children: [{ name: "C1" }, { name: "C2" }],
      },
    ],
  },
  {
    name: "A1",
    children: [
      {
        name: "B1",
        children: [{ name: "B11" }, { name: "B21" }],
      },
      {
        name: "C1",
        children: [{ name: "C11" }, { name: "C21" }],
      },
    ],
  },
];

bfs(root)

数组

数组是一种线性的数据结构
优点:查找特定的元素特别快，通过索引下标查找元素，时间复杂度 O(1)
缺点:需要在内存中开辟连续的空间，当达到上限的时候，需要开辟 2 倍的空间，在把之前的数组拷贝过去,在头部增加、删除元素特别慢，因为每一个元素都需要位移

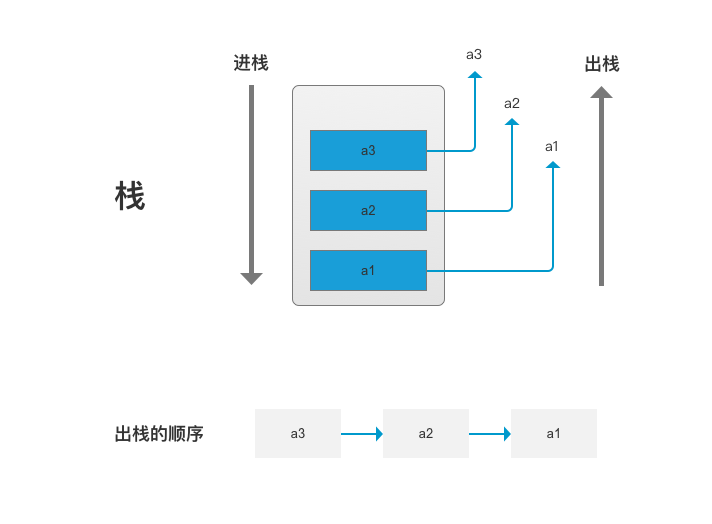
栈

栈是一种受限的数据结构，可以用数组或者链表来实现
特点：后进的先出，分为进栈和出栈，只能从栈顶一端进行操作，不能跨级

stack

class Stack {
  constructor() {
    this.items = [];
  }
  // 进栈
  push(element) {
    this.items.push(element);
  }
  // 出栈
  pop() {
    return this.items.pop();
  }
  // 查看栈顶元素
  peek() {
    return this.items[this.items.length - 1];
  }
  // 获取栈中元素的个数
  size() {
    return this.items.length;
  }
  // 判断栈中的元素是否为空
  isEmpty() {
    return this.items.length === 0;
  }
  toString() {
    return this.items.join(",");
  }
}

十进制转二进制

function dec2bin(decNumer) {
  let stack = new Stack();
  let n = decNumer;
  while (n > 0) {
    n = Math.floor(n / 2);
    stack.push(n % 2);
  }
  let binayriStrng = "";
  while (!stack.isEmpty()) {
    binayriStrng = binayriStrng + "" + stack.pop();
  }
  return binayriStrng;
}

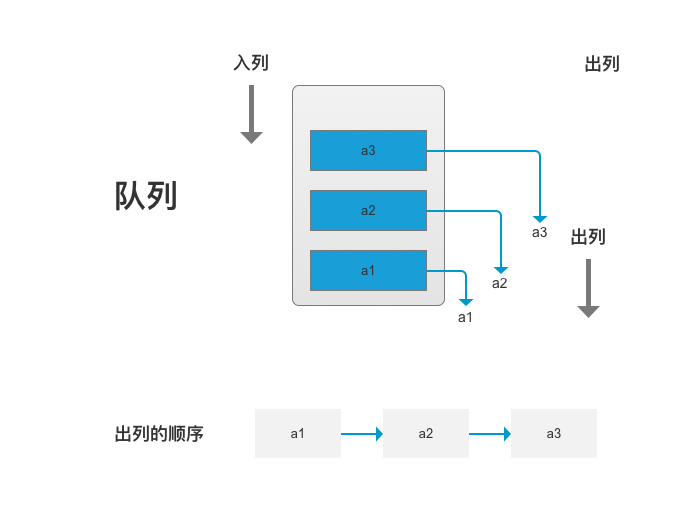
队列

队列是一种受限的数据结构
特点：队列是从 2 端进行操作，一边进一边出，先进的先出，在加入队列的时候可以设置优先级，优先级越高位置越前

queue

普通队列

class Queue {
  constructor() {
    this.items = [];
  }
  // 入列
  enqueue(element) {
    this.items.push(element);
  }
  // 出列
  dequeue() {
    return this.items.shift();
  }
  // 查看队列顶元素
  front() {
    return this.items[0];
  }
  // 获取队列中元素的个数
  size() {
    return this.items.length;
  }
  // 判断队列中的元素是否为空
  isEmpty() {
    return this.items.length === 0;
  }
  toString() {
    return this.items.join(",");
  }
}

优先级队列

class PriorityQueue {
  constructor() {
    this.items = [];
  }
  // 入列
  enqueue(element, priority) {
    let enqueueItem = { element, priority };
    if (this.isEmpty()) {
      this.items.push(enqueueItem);
    } else {
      let hasAdd = false;
      for (let index = 0; index < this.items.length; index++) {
        // 数组越小优先级越高
        if (priority < this.items[index].priority) {
          this.items.splice(index, 0, enqueueItem);
          hasAdd = true;
          break;
        }
      }
      // 遍历结束还未插入
      if (!hasAdd) {
        this.items.push(enqueueItem);
      }
    }
  }
  // 出列
  dequeue() {
    return this.items.shift();
  }
  // 查看队列顶元素
  front() {
    return this.items[0];
  }
  // 获取队列中元素的个数
  size() {
    return this.items.length;
  }
  // 判断队列中的元素是否为空
  isEmpty() {
    return this.items.length === 0;
  }
  toString() {
    return JSON.stringify(this.items);
  }
}

// 有n个人，从1到y开始数数，每次数到y的人被淘汰，请问最后一个人谁，在原来的什么位置
function game(nameList, num) {
  let queue = new Queue();
  nameList.forEach((name) => {
    queue.enqueue(name);
  });
  while (queue.size() > 1) {
    for (var i = 1; i < num; i++) {
      queue.enqueue(queue.dequeue());
    }
    console.log(queue.dequeue());
  }
  let index = nameList.indexOf(queue.toString());
  console.log(`最终留下来的人${queue.toString()},原来${index}的位置`);
}
let nameList = ["lisi", "wangwu", "xianming", "tom"];
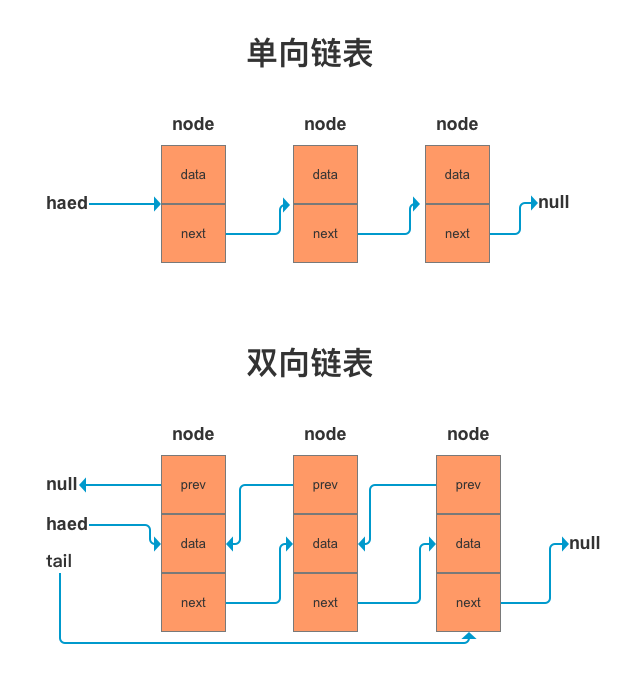
game(nameList, 3);

链表

链表和数组一样，可以存储一系列的元素，但是底层实现和数组完全不同
特点：
- 1、内存空间不是连续的，可以动态的利用内存
- 2、在创建的时候不必确定大小，并且可以无限的延伸下去
- 3、插入和删除数据时间复杂度可以达到 O(1)
缺点：
- 无法直接通过索引直接找到对应的元素，需要遍历

linkedList

单向链表

class LinkedList {
  constructor() {
    this.head = null;
    this.length = 0;
  }

  // 链表元素
  node(element) {
    return {
      element: element,
      next: null,
    };
  }

  // 链表尾部添加数组
  append(element) {
    let newNode = this.node(element);
    // 如果没有数据
    if (this.head == null) {
      this.head = newNode;
    } else {
      // 遍历找到最后一个元素
      let currentNode = this.head;
      while (currentNode.next) {
        currentNode = currentNode.next;
      }
      // 追加元素
      currentNode.next = newNode;
    }
    this.length++;
  }

  // 指定的位置插入数据
  insert(position, element) {
    // 越界判断
    if (position < 0 || position > this.length)
      throw Error("LinkedListInsertBoundsException");
    let newNode = this.node(element);
    let currentNode = this.head;
    let prevNode = null;
    let index = 0;
    // 如果是第一个
    if (position === 0) {
      newNode.next = currentNode;
      this.head = newNode;
    } else {
      // 循环找到当前的要插入的位置
      while (index < position) {
        prevNode = currentNode;
        currentNode = currentNode.next;
        index++;
      }
      // 改变指针指向
      newNode.next = currentNode;
      prevNode.next = newNode;
    }
    this.length++;
    return true;
  }

  // 根据指定的位置删除元素
  removeAt(position) {
    // 越界判断
    if (position < 0 || position >= this.length)
      throw Error("LinkedListInsertBoundsException");
    let currentNode = this.head;
    let prevNode = null;
    let index = 0;
    // 如果是第一个
    if (position === 0) {
      this.head = currentNode.next;
    } else {
      // 循环找到当前的要删除的位置
      while (index < position) {
        prevNode = currentNode;
        currentNode = currentNode.next;
        index++;
      }
      // 改变指针指向
      prevNode.next = currentNode.next;
    }
    this.length--;
    return currentNode.element;
  }

  // 根据元素去查找元素指定的位置
  indexOf(element) {
    let currentNode = this.head;
    let index = 0;
    while (currentNode) {
      if (currentNode.element === element) {
        return index;
      }
      currentNode = currentNode.next;
      index++;
    }
    return -1;
  }

  // 根据元素删除元素
  remove(element) {
    let position = this.indexOf(element);
    return this.removeAt(position);
  }

  toString() {
    let currentNode = this.head;
    let nodeStr = "";
    while (currentNode) {
      nodeStr += "|" + currentNode.element;
      currentNode = currentNode.next;
    }
    return nodeStr.slice(1);
  }

  isEmpty() {
    return this.length === 0;
  }

  size() {
    return this.length;
  }

  // 查询头部元素
  getFirst() {
    return this.head.element;
  }
}

反转链表

function reverseLinkedListIterative(head) {
 
  let preNode = null; // 上一个
  let currentNode = head; // 当前的
  while(currentNode){
    let nextNode = currentNode.next; // 保留后续的链表，防止冲断
    currentNode.next = preNode // 让下一个节点，指向上一个节点
    preNode = currentNode // 让上一个节点指向当前的节点
    currentNode = nextNode // 继续循环
  }
  return preNode
}

console.log(reverseLinkedListIterative(linkedList.head))

双向链表

class DoubleLinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.length = 0;
  }

  // 链表元素
  node(element) {
    return {
      element: element,
      prev: null,
      next: null,
    };
  }

  // 二分查找
  binarySearch(position) {
    if (this.length / 2 > position) {
      return {
        type: "front",
        position: position,
      };
    } else {
      return {
        type: "back",
        position: this.length - position,
      };
    }
  }

  // 链表尾部添加数组
  append(element) {
    let newNode = this.node(element);
    // 如果没有数据
    if (this.head == null) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      // 遍历找到最后一个元素
      let currentNode = this.head;
      while (currentNode.next) {
        currentNode = currentNode.next;
      }
      // 追加元素
      newNode.prev = currentNode;
      currentNode.next = newNode;
      this.tail = newNode;
    }
    this.length++;
  }

  // 指定的位置插入数据
  insert(position, element) {
    // 越界判断
    if (position < 0 || position > this.length)
      throw Error("LinkedListInsertBoundsException");
    let newNode = this.node(element);
    // 如果是第一个
    if (position === 0) {
      // 数据为空
      if (this.head == null) {
        this.head = newNode;
        this.tail = newNode;
      } else {
        this.head.prev = newNode;
        newNode.next = this.head;
        this.head = newNode;
      }
    } else if (position === this.length) {
      // 如果是最后一个
      this.tail.next = newNode;
      newNode.prev = this.tail;
      this.tail = newNode;
    } else {
      let previous = null;
      let currentNode = null;
      let binarySearch = this.binarySearch(position);
      let index = 0;
      // 正向
      if (binarySearch.type === "front") {
        currentNode = this.head;
        // 循环找到当前的要插入的位置
        while (index < position) {
          previous = currentNode;
          currentNode = currentNode.next;
          index++;
        }
        // 交换节点的指向顺序
        newNode.next = currentNode;
        newNode.prev = previous;
        currentNode.prev = newNode;
        previous.next = newNode;
      } else {
        // 反向
        currentNode = this.tail;
        while (index < binarySearch.position) {
          previous = currentNode;
          currentNode = currentNode.prev;
          index++;
        }
        // 交换节点的指向顺序
        newNode.next = previous;
        newNode.prev = currentNode;
        currentNode.next = newNode;
        previous.prev = newNode;
      }
    }
    this.length++;
    return true;
  }

  // 根据指定的位置删除元素
  removeAt(position) {
    // 越界判断
    if (position < 0 || position >= this.length)
      throw Error("LinkedListInsertBoundsException");
    let currentNode = this.head;
    // 如果是第一个
    if (position === 0) {
      // 只有一个数组
      if (this.length === 1) {
        this.head = null;
        this.tail = null;
      } else {
        this.head = this.head.next;
        this.head.prev = null;
      }
    } else if (position === this.length - 1) {
      // 如果最后一个
      currentNode = this.tail;
      this.tail = this.tail.prev;
      this.tail.next = null;
    } else {
      let previous = null;
      let binarySearch = this.binarySearch(position);
      let index = 0;
      if (binarySearch.type === "front") {
        // 正向
        while (index < position) {
          previous = currentNode;
          currentNode = currentNode.next;
          index++;
        }
        previous.next = currentNode.next;
        currentNode.next.prev = previous;
        this.length--;
        return currentNode.element;
      } else {
        currentNode = this.tail;
        // 反向
        while (index < binarySearch.position) {
          previous = currentNode;
          currentNode = currentNode.prev;
          index++;
        }
        currentNode.next = previous.next;
        previous.next.prev = currentNode;
        this.length--;
        return previous.element;
      }
    }
  }

  // 根据元素去查找元素指定的位置
  indexOf(element) {
    let currentNode = this.head;
    let index = 0;
    while (currentNode) {
      if (currentNode.element === element) {
        return index;
      }
      currentNode = currentNode.next;
      index++;
    }
    return -1;
  }

  // 根据元素删除元素
  remove(element) {
    let position = this.indexOf(element);
    return this.removeAt(position);
  }

  isEmpty() {
    return this.length === 0;
  }

  size() {
    return this.length;
  }

  // 查询头部元素
  getHead() {
    return this.head.element;
  }

  // 查询尾部元素
  getTail() {
    return this.tail.element;
  }

  // 正向遍历
  forwardString() {
    let currentNode = this.head;
    let nodeStr = "";
    while (currentNode) {
      nodeStr += "|" + currentNode.element;
      currentNode = currentNode.next;
    }
    return nodeStr.slice(1);
  }

  // 反向遍历
  reverseString() {
    let currentNode = this.tail;
    let nodeStr = "";
    while (currentNode) {
      nodeStr += "|" + currentNode.element;
      currentNode = currentNode.prev;
    }
    return nodeStr.slice(1);
  }

  toString() {
    return this.forwardString();
  }
}

集合

集合和数组内似，可以存储多个数据，它的无序的，并且不能重复(后添加的会覆盖前面的)

class Set {
  constructor() {
    this.items = {};
  }

  // 判断集合中是否有某个元素
  has(value) {
    return this.items.hasOwnProperty(value);
  }

  // 向集合中添加元素
  add(value) {
    this.items[value] = value;
    return true;
  }

  // 从集合中删除某个元素
  remove(value) {
    if (this.has(value)) {
      delete this.items[value];
      return true;
    }
    return false;
  }

  // 清空集合中所有的元素
  clear() {
    this.items = {};
  }

  // 获取集合的大小
  size() {
    return Object.keys(this.items).length;
  }

  // 获取集合中所有的值
  values() {
    return Object.keys(this.items);
  }
}

字典

字典，可以存储多个数据，它的无序的，并且不能重复((后添加的会覆盖前面的)key,value 形式)

class Dictionay {
  constructor() {
    this.items = {};
  }

  // 判断字典中是否包含某个key
  has(key) {
    return this.items.hasOwnProperty(key);
  }

  // 在字典中添加键值对
  set(key, value) {
    this.items[key] = value;
    return true;
  }

  // 根据key去获取value
  get(key) {
    return this.has(key) ? this.items[key] : undefined;
  }

  // 从字典中移除元素
  remove(key) {
    if (this.has(key)) {
      delete this.has(key);
      return true;
    }
    return false;
  }

  // 获取所有的keys
  keys() {
    return Object.keys(this.items);
  }

  // 获取所有的value
  values() {
    return Object.values(this.items);
  }

  // size方法
  size() {
    return this.keys().length;
  }

  // clear方法
  clear() {
    this.items = {};
  }
}

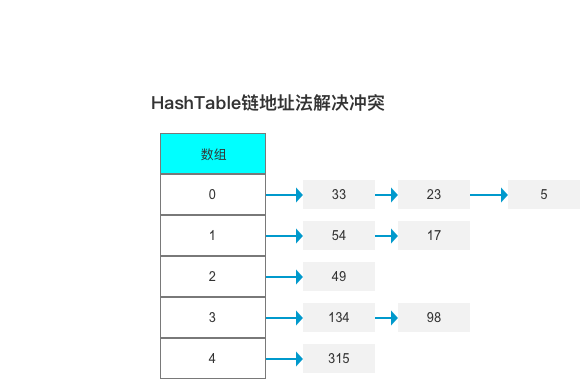
哈希表

特点：增加和删除都比较高，可以达到瞬间查找
缺点：无法直接进行遍历，元素不能重复
实现原理:利用数组实现，当在存值的时候，首先把 key 作为条件，生成一个 hashCode 码，hashCode 码作为数组的索引，插入到二维数组中(链地址法解决冲突)

hashTable

class HashTable {
  constructor() {
    this.storage = [];
    this.count = 0;
    this.limit = 8;
  }

  // 哈希函数
  hashFunc(str, max) {
    let hashCode = 0;
    // 霍纳算法, 来计算hashCode的数值
    for (let index = 0; index < str.length; index++) {
      // 质树有利于平均分布
      hashCode = 37 * hashCode + str.charCodeAt(index);
    }
    //压缩到指定的索引范围
    return hashCode % max;
  }

  // 判断是否是质数
  isPrime(num) {
    let temp = parseInt(Math.sqrt(num));
    for (let index = 2; index <= temp; index++) {
      if (num % index === 0) {
        return false;
      }
      return true;
    }
  }

  getPrime(num) {
    if (!this.isPrime(num)) return this.getPrime(++num);
    return num;
  }

  put(key, value) {
    // 生成索引
    let index = this.hashFunc(key, this.limit);
    let bucket = this.storage[index];
    if (bucket === undefined) {
      bucket = [];
      this.storage[index] = bucket;
    }
    let override = false;
    for (let i = 0; i < bucket.length; i++) {
      let temp = bucket[i];
      // 判断是否存在
      if (temp[0] === key) {
        temp[1] = value;
        override = true;
      }
    }
    // 不存在直接追加
    if (!override) {
      bucket.push([key, value]);
      this.count++;
      // 总长度超过限制的75%,需要扩容
      if (this.count > this.limit * 0.75) {
        this.resize(this.getPrime(this.limit * 2));
      }
    }
  }

  get(key) {
    let index = this.hashFunc(key, this.limit);
    let bucket = this.storage[index];
    if (bucket === undefined) {
      return null;
    }
    for (let i = 0; i < bucket.length; i++) {
      const temp = bucket[i];
      if (temp[0] === key) {
        return temp[1];
      }
    }
    return null;
  }

  remove(key) {
    let index = this.hashFunc(key, this.limit);
    let bucket = this.storage[index];
    if (bucket == undefined) {
      return null;
    }
    for (let i = 0; i < bucket.length; i++) {
      const temp = bucket[i];
      if (temp[0] === key) {
        bucket.splice(i, 1);
        this.count--;
        // 总长度小于限制的25%,需要缩小数组的容量
        if (this.limit > 7 && this.count < this.limit * 0.25) {
          this.resize(this.getPrime(Math.floor(this.limit / 2)));
        }
        return temp[1];
      }
      return null;
    }
  }

  resize(newLimit) {
    let oldStorage = this.storage;
    // 属性重置
    this.storage = [];
    this.limit = newLimit;
    this.count = 0;
    for (let index = 0; index < oldStorage.length; index++) {
      let arr = oldStorage[index];
      if (arr !== undefined) {
        arr.forEach((bucket) => {
          this.put(bucket[0], bucket[1]);
        });
      }
    }
  }

  isEmpty() {
    return this.count == 0;
  }

  size() {
    return this.count;
  }
}

二叉树

树的定义

树（Tree）: n（n≥0）个结点构成的有限集合。
当 n=0 时，称为空树；
对于任一棵非空树（n> 0），它具备以下性质：
- 树中有一个称为“根（Root）”的特殊结点，用 r 表示；
- 其余结点可分为 m(m>0)个互不相交的有限集 T1，T2，... ，Tm，其中每个集合本身又是一棵树，称为原来树的“子树（SubTree）”
注意:
子树之间不可以相交
除了根结点外，每个结点有且仅有一个父结点；

树的术语

1.结点的度（Degree）：结点的子树个数.
2.树的度：树的所有结点中最大的度数. (树的度通常为结点的个数 N-1)
3.叶结点（Leaf）：度为 0 的结点. (也称为叶子结点)
4.父结点（Parent）：有子树的结点是其子树的根结点的父结点
5.子结点（Child）：若 A 结点是 B 结点的父结点，则称 B 结点是 A 结点的子结点；子结点也称孩子结点。
6.兄弟结点（Sibling）：具有同一父结点的各结点彼此是兄弟结点。
7.路径和路径长度：从结点 n1 到 nk 的路径为一个结点序列 n1 , n2,… , nk, ni 是 ni+1 的父结点。路径所包含边的个数为路径的长度。
8.结点的层次（Level）：规定根结点在 1 层，其它任一结点的层数是其父结点的层数加 1。
9.树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度。

二叉树的特性

一个二叉树第 i 层的最大结点数为：2^(i-1), i >= 1;
深度为 k 的二叉树有最大结点总数为： 2^k - 1, k >= 1;
对任何非空二叉树 T，若 n0 表示叶结点的个数、n2 是度为 2 的非叶结点个数，那么两者满足关系 n0 = n2 + 1。
完美二叉树(Perfect Binary Tree) , 也称为满二叉树(Full Binary Tree）
在二叉树中, 除了最下一层的叶结点外, 每层节点都有 2 个子结点, 就构成了满二叉树.
完全二叉树(Complete Binary Tree)
除二叉树最后一层外, 其他各层的节点数都达到最大个数.
且最后一层从左向右的叶结点连续存在, 只缺右侧若干节点.
完美二叉树是特殊的完全二叉树.
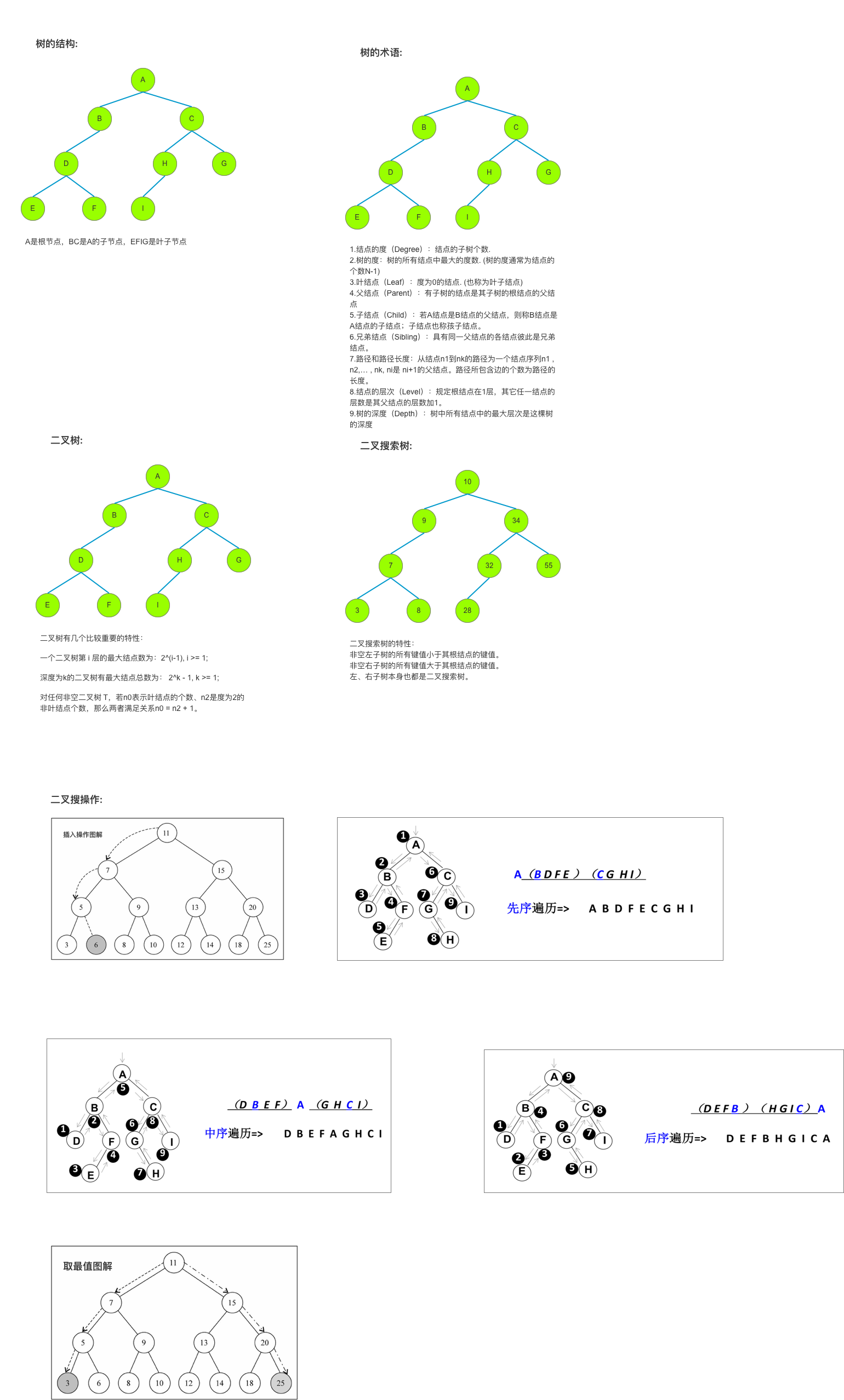
二叉搜索树的特点:
二叉搜索树的特点就是相对较小的值总是保存在左结点上, 相对较大的值总是保存在右结点上.

class BinarySerachTree {
  constructor() {
    this.root = null;
  }

  node(key) {
    return {
      key: key,
      left: null,
      right: null,
    };
  }

  // 插入操作
  insert(key) {
    let newNode = this.node(key);
    if (this.root === null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }
  }

  insertNode(node, newNode) {
    // 小于向左找
    if (newNode.key < node.key) {
      // 如果没左节点
      if (node.left === null) {
        node.left = newNode;
      } else {
        // 如果有左节点，递归
        this.insertNode(node.left, newNode);
      }
    } else {
      if (node.right === null) {
        node.right = newNode;
      } else {
        this.insertNode(node.right, newNode);
      }
    }
  }

  /**
   * 深度优先遍历-先序遍历
   * ①访问根结点；
   * ②先序遍历其左子树；
   * ③先序遍历其右子树
   */

  preOrderTraverse(handler) {
    this.preOrderTraverseNode(this.root, handler);
  }

  preOrderTraverseNode(node, handler) {
    if (node !== null) {
      handler(node.key);
      this.preOrderTraverseNode(node.left, handler);
      this.preOrderTraverseNode(node.right, handler);
    }
  }

  /**
   * 深度优先遍历-中序遍历
   * ①中序遍历其左子树；
   * ②访问根结点；
   * ③中序遍历其右子树。
   */
  inOrderTraversal(handler) {
    this.inOrderTraversalNode(this.root, handler);
  }

  inOrderTraversalNode(node, handler) {
    if (node !== null) {
      this.inOrderTraversalNode(node.left, handler);
      handler(node.key);
      this.inOrderTraversalNode(node.right, handler);
    }
  }

  /**
   * 深度优先遍历-后序遍历
   * ①后序遍历其左子树；
   * ②后序遍历其右子树；
   * ③访问根结点。
   */
  postOrderTraversal(handler) {
    this.postOrderTraversalNode(this.root, handler);
  }

  postOrderTraversalNode(node, handler) {
    if (node !== null) {
      this.postOrderTraversalNode(node.left, handler);
      this.postOrderTraversalNode(node.right, handler);
      handler(node.key);
    }
  }

  // 删除节点
  remove(key) {
    let current = this.root;
    let parent = null;
    let isLeftChild = true;
    while (current.key != key) {
      parent = current;
      if (key > current.key) {
        isLeftChild = false;
        current = current.right;
      } else {
        isLeftChild = true;
        current = current.left;
      }
      // 如果current已经指向null, 那么说明没有找到要删除的数据
      if (current === null) return false;
    }

    // 情况一:如果是叶节点
    if (current.left === null && current.right === null) {
      // 正好的根节点
      if (current === this.root) {
        this.root = null;
      } else if (isLeftChild) {
        parent.left = null;
      } else {
        parent.right = null;
      }
    }
    // 情况二:只有一个节点
    else if (current.left === null) {
      // 如果是根节点
      if (current === this.root) {
        this.root = current.right;
      } else if (isLeftChild) {
        parent.left = current.right;
      } else {
        parent.right = current.right;
      }
    } else if (current.right === null) {
      // 如果是根节点
      if (current === this.root) {
        this.root = current.left;
      } else if (isLeftChild) {
        parent.left = current.left;
      } else {
        parent.right = current.left;
      }
    } else {
      /**
       * 删除有两个节点的节点(操作完成后还需要满足二叉搜索数的特性)
       * 方案一：把当前要删除的左子数最大的提取上去(前驱)
       * 方案二：把当前要删除的右子数最小的提取上去(后继)
       */
      let successor = this.getSuccessor(current);
      if (current === this.root) {
        this.root = successor;
      } else if (isLeftChild) {
        parent.left = successor;
      } else {
        parent.right = successor;
      }
      successor.left = current.left;
    }
    return true;
  }

  // 找后继的方法
  getSuccessor(delNode) {
    let successorParent = delNode;
    let successor = delNode;
    let current = delNode.right; // 要从右子树开始找

    while (current != null) {
      successorParent = successor;
      successor = current;
      current = current.left;
    }

    // 如果提取上去的节点有子节点
    if (successor != delNode.right) {
      successorParent.left = successor.right;
      successor.right = delNode.right;
    }

    return successor;
  }

  // 搜搜特定的值
  search(key) {
    let node = this.root;
    while (node !== null) {
      if (key < node.key) {
        node = node.left;
      } else if (key > node.key) {
        node = node.right;
      } else {
        return node;
      }
    }
    return null;
  }

  // 或取最小值
  min() {
    let node = this.root;
    while (node.left !== null) {
      node = node.left;
    }
    return node.key;
  }
  // 或取最大值
  max() {
    let node = this.root;
    while (node.right !== null) {
      node = node.right;
    }
    return node.key;
  }
}

// 测试代码
var bst = new BinarySerachTree();

// 插入数据
bst.insert(10);
bst.insert(9);
bst.insert(34);
bst.insert(7);
bst.insert(3);
bst.insert(8);
bst.insert(32);
bst.insert(55);
bst.insert(28);
let stra = "";
console.log(bst.remove(10));
bst.preOrderTraverse((key) => {
  stra = stra + " " + key;
});
console.log("先序", stra);

let strb = "";
bst.inOrderTraversal((key) => {
  strb = strb + " " + key;
});
console.log("中序", strb);
let strc = "";
bst.postOrderTraversal((key) => {
  strc = strc + " " + key;
});
console.log("后序", strc);

冒泡排序

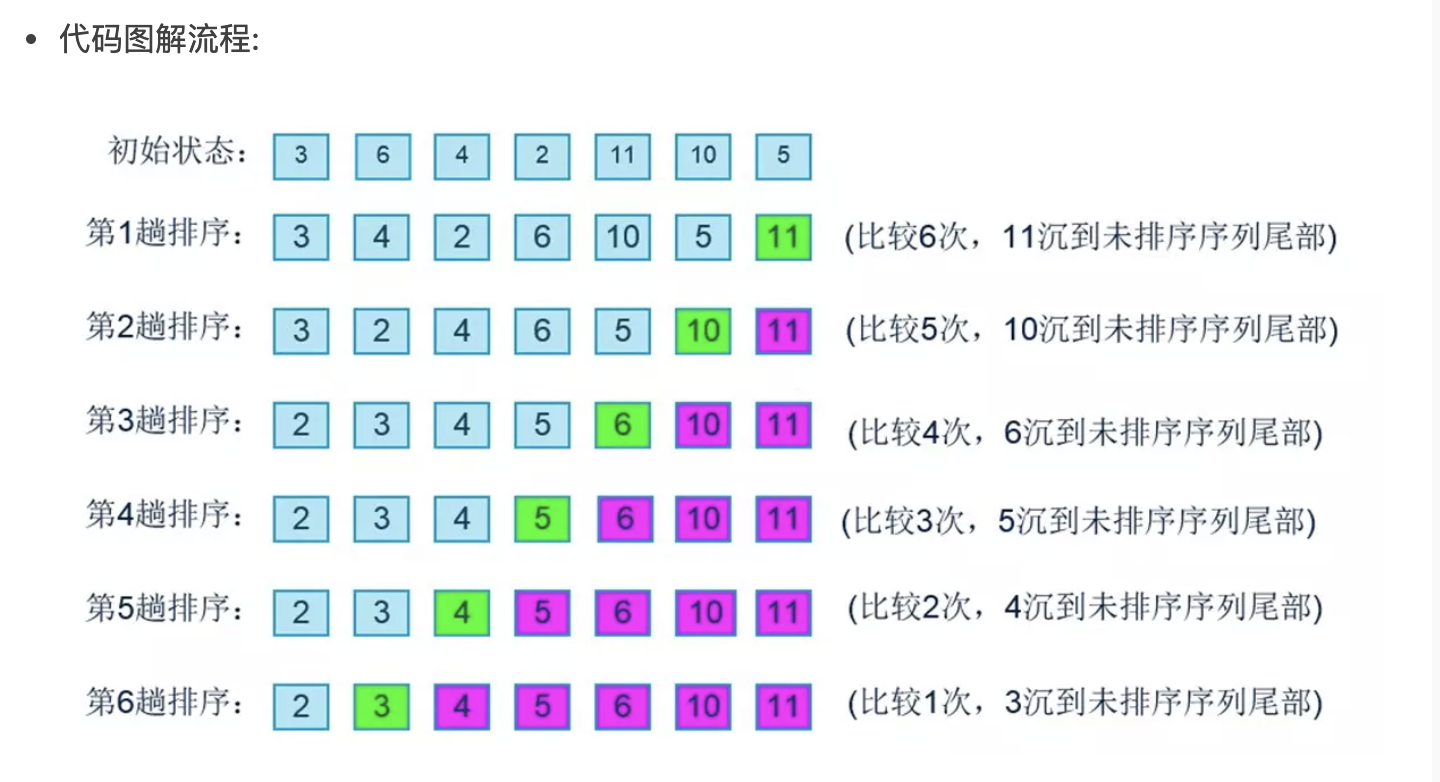
思路:
- 每相邻的二个元素进行比较如果大于就交换顺序
- 第一次找出最高的一位放置在末尾
- 第二次找出次高的一位放置在倒数第二，依次内推
代码实现:
- 外层循环控制每次对比的次数，对比的次数依次减少
- 内层循环两两进行对比，内外层循环结束顺序就依次排列好
时间复杂度:
- 对比的次数和交换的次数都是 O(N^2)

bubbleSort

class ArrayList {
  constructor() {
    this.array = [];
  }
  insert(item) {
    this.array.push(item);
  }
  toString() {
    return this.array.join(",");
  }
  // 交换
  swap(x, y) {
    let temp = this.array[x];
    this.array[x] = this.array[y];
    this.array[y] = temp;
  }

  bubbleSort() {
    let len = this.array.length;
    for (let i = 0; i < len - 1; i++) {
      for (let j = i + 1; j < len; j++) {
        if (this.array[i] > this.array[j]) {
          this.swap(i, j);
        }
      }
    }
  }
}

let arrayList = new ArrayList();
arrayList.insert(3);
arrayList.insert(6);
arrayList.insert(4);
arrayList.insert(2);
arrayList.insert(11);
arrayList.insert(10);
arrayList.insert(5);
arrayList.bubbleSort();
console.log(arrayList.toString()); // 2,3,4,5,6,10,11

选择排序

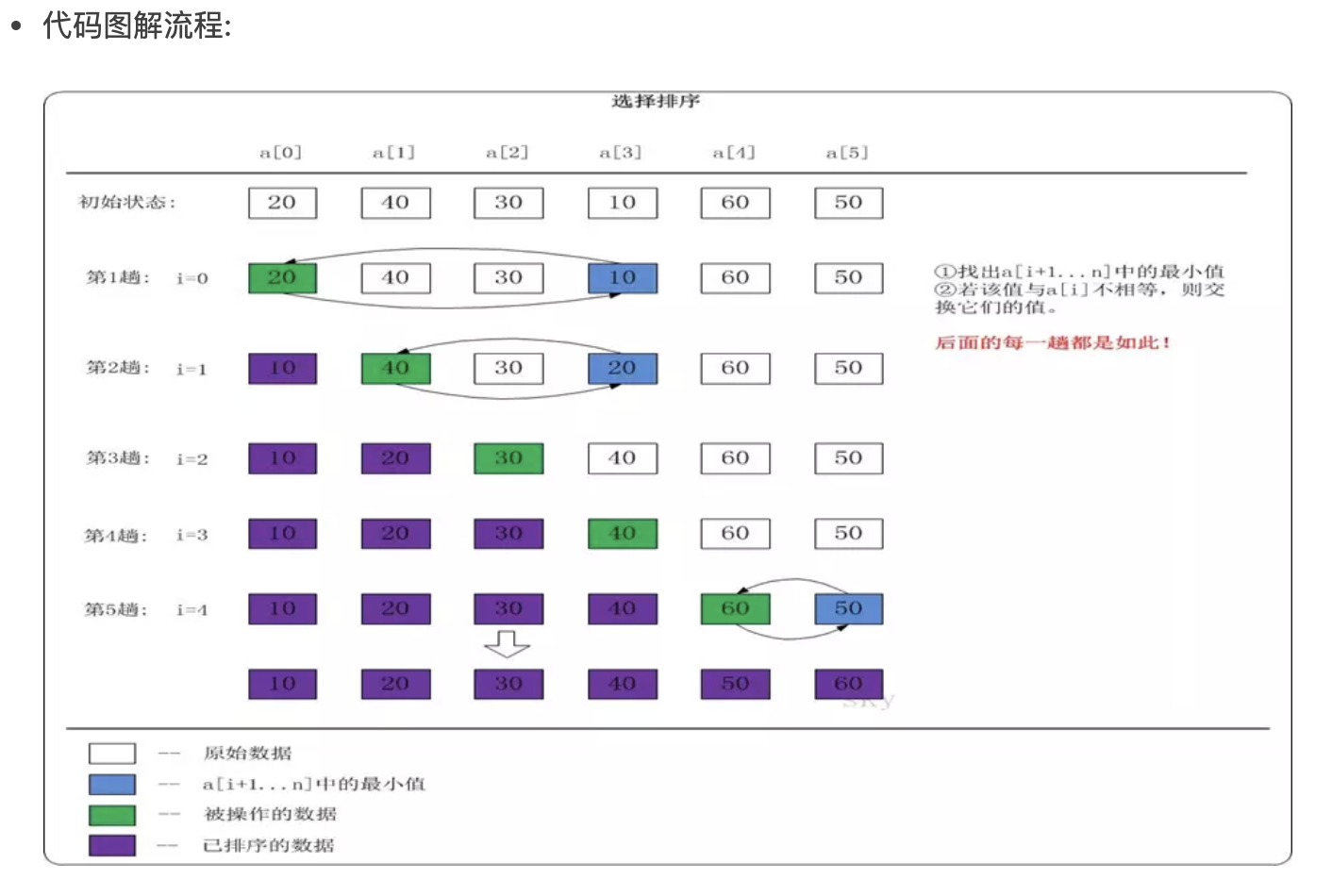
思路:
- 选择第一个索引的位置，依次和后面的进行比较
- 如果大于就交换它们的位置，循环到最后，就能确定最小的位置的索引
- 用最小位置的索引的值和第一个索引进行交换，依次内推
代码实现:
- 外层循环记录需要交换的索引位置，每次交换后需要从下一个索引开始，所以依次递增
- 内层循环依次进行对比找出最小的值的索引，内层循环结束后交换值位置
时间复杂度:
- 对比的次数 O(N^2)
- 交换的次数都是 O(N)

selectionSort

class ArrayList {
  constructor() {
    this.array = [];
  }
  insert(item) {
    this.array.push(item);
  }
  toString() {
    return this.array.join(",");
  }
  // 交换
  swap(x, y) {
    let temp = this.array[x];
    this.array[x] = this.array[y];
    this.array[y] = temp;
  }

  selectionSort() {
    let len = this.array.length;
    for (let i = 0; i < len - 1; i++) {
      let min = i;
      // 内循环找出最小的值的索引
      for (let j = i + 1; j < len; j++) {
        if (this.array[min] > this.array[j]) {
          min = j;
        }
      }
      // 交换
      this.swap(i, min);
    }
  }
}

let arrayList = new ArrayList();
arrayList.insert(20);
arrayList.insert(40);
arrayList.insert(30);
arrayList.insert(10);
arrayList.insert(60);
arrayList.insert(50);
arrayList.selectionSort();
console.log(arrayList.toString()); // 10,20,30,40,50,60

插入排序

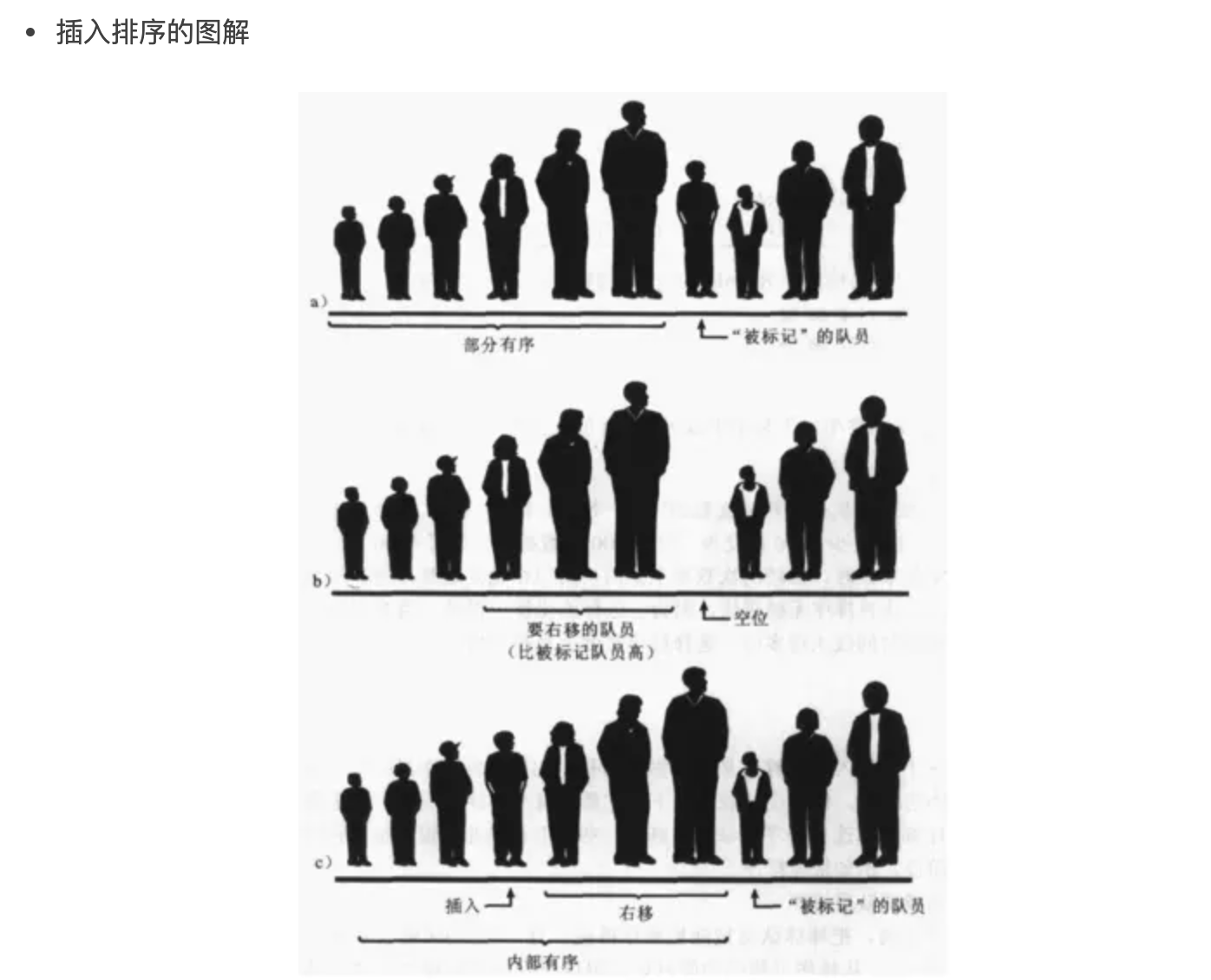
insertionSort

思路:
- 从下标一开始，默认 0 的位置可以看成局部有序
- 从第一个开始依次往前进行对比，大于就交换顺序，直到对比到第一个下标的位置
代码实现:
- 外层循环控制对比的次数，记录索引的位置和值，索引依次递增
- 内层循环进行对比，大于就直接赋值，并且记录索引的位置
- 内层循环结束后，录索引的位置进行赋值
时间复杂度:
- 对比的次数 O(N^2)
- 交换的次数都是 O(N)

class ArrayList {
  constructor() {
    this.array = [];
  }

  insert(item) {
    this.array.push(item);
  }

  toString() {
    return this.array.join(",");
  }

  // 交换
  swap(x, y) {
    let temp = this.array[x];
    this.array[x] = this.array[y];
    this.array[y] = temp;
  }

  insertionSort() {
    const len = this.array.length;
    for (let i = 1; i < len; i++) {
      let j = i;
      let temp = this.array[i];
      while (j > 0 && this.array[j - 1] > temp) {
        this.array[j] = this.array[j - 1];
        j--;
      }
      this.array[j] = temp;
    }
  }
}

let array = new ArrayList();
array.insert(10);
array.insert(1);
array.insert(20);
array.insert(4);
array.insertionSort(array);
console.log(array.toString());

希尔排序

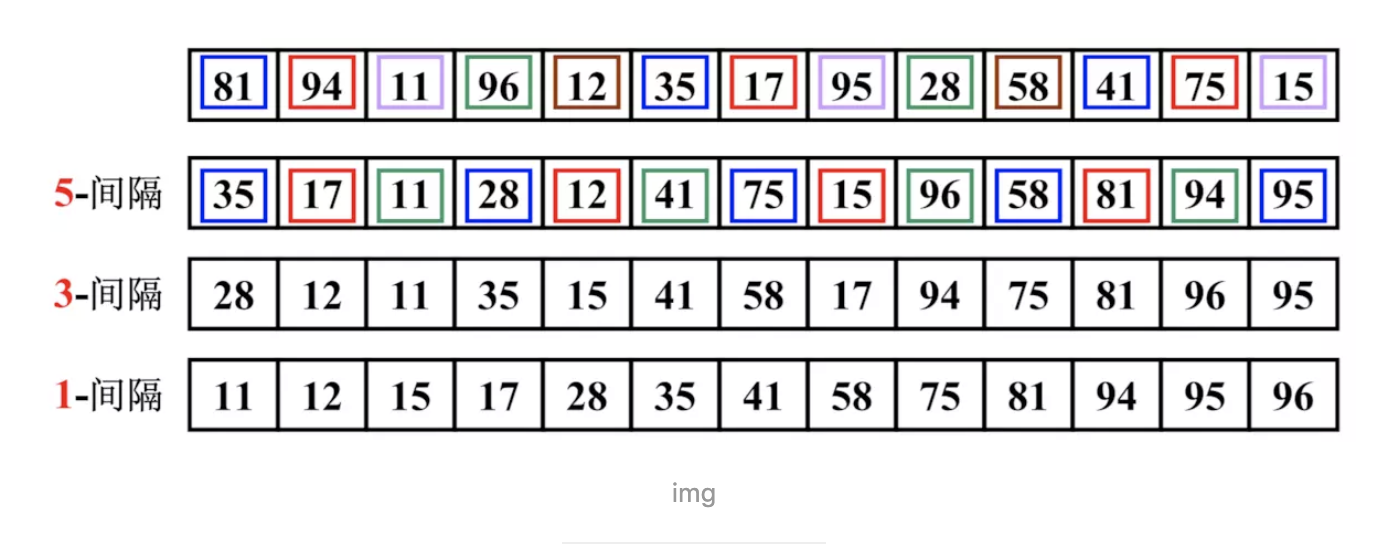
希尔排序(插入排序升级版)
- 首先获取一个增量
- 外层循环增量不断变小, 大于 0 就继续改变增量
- 内层循环实现了插入排序
时间复杂度:
- 最坏的情况 O(N^2)

shellSort

class ArrayList {
  constructor() {
    this.array = [];
  }

  insert(item) {
    this.array.push(item);
  }

  toString() {
    return this.array.join(",");
  }

  // 交换
  swap(x, y) {
    let temp = this.array[x];
    this.array[x] = this.array[y];
    this.array[y] = temp;
  }

  shellSort() {
    const len = this.array.length;
    let gap = Math.floor(len / 2);
    while (gap > 0) {
      for (let i = gap; i < this.array.length; i++) {
        let j = i;
        let temp = this.array[i];
        while (j > gap - 1 && this.array[j - gap] > temp) {
          this.array[j] = this.array[j - gap];
          j -= gap;
        }
        this.array[j] = temp;
      }
      gap = Math.floor(gap / 2);
    }
  }
}

let array = new ArrayList();
array.insert(10);
array.insert(1);
array.insert(20);
array.insert(4);
array.quickSort(array);
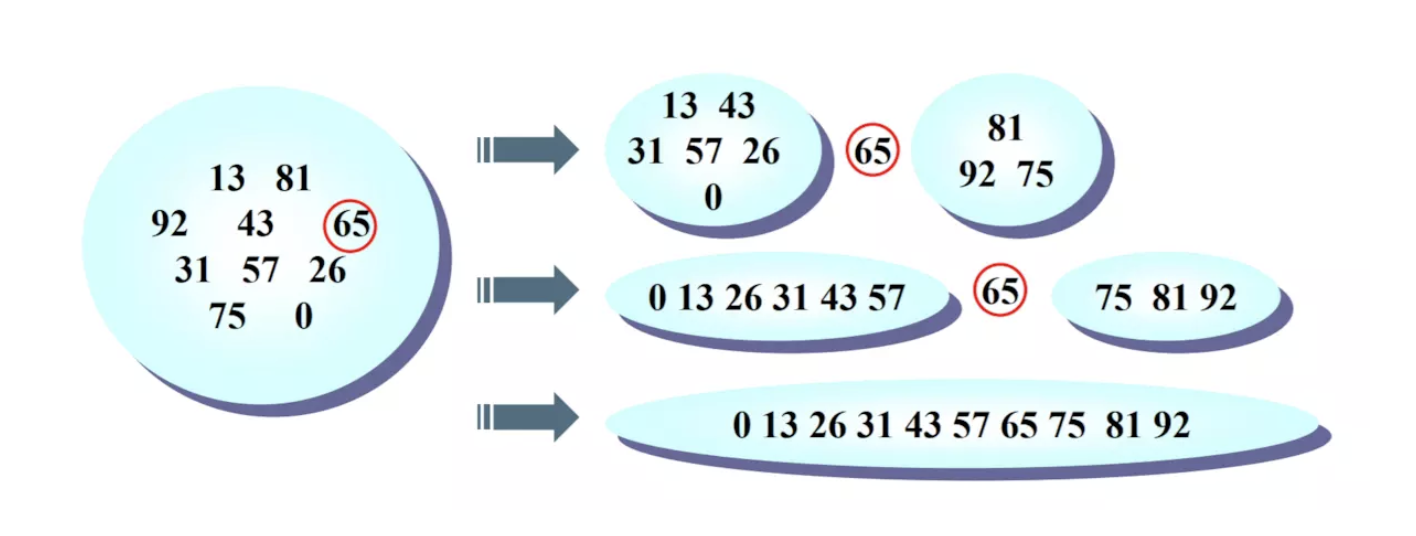
console.log(array.toString());

快速排序

思路
- 选择第一位最为枢纽
- 从第二位开始进行遍历
- 比枢纽小的放在左边，小的放在右边，此时枢纽就是正确的位置
- 左边、右边也是一个数组，在进行递归，所有的递归结束后就排好顺序
时间复杂度
- O(N*logN)

quick

class ArrayList {
  constructor() {
    this.array = [];
  }

  insert(item) {
    this.array.push(item);
  }

  toString() {
    return this.array.join(",");
  }

  quick(list) {
    if (!Array.isArray(list)) {
      return list;
    }

    if (list.length === 0) {
      return [];
    }
    let pivot = list[0];
    let mins = [];
    let maxs = [];
    for (let index = 1; index < list.length; index++) {
      let item = list[index];
      if (pivot > item) {
        mins.push(item);
      } else {
        maxs.push(item);
      }
    }

    return [...this.quick(mins), pivot, ...this.quick(maxs)];
  }

  quickSort() {
    this.array = this.quick(this.array);
  }
}

let array = new ArrayList();
array.insert(10);
array.insert(1);
array.insert(20);
array.insert(4);
array.quickSort();
console.log(array.toString());

二分查找

思路
- 每次取从中间的位置开始
- 如果找到返回索引
- 如果中间的数值大，继续从左找
- 如果中间的数值小，继续从右找
- 循环结束后还未找到返回-1
时间复杂度
- O(N*logN)

class ArrayList {
  constructor() {
    this.array = [];
  }

  insert(item) {
    this.array.push(item);
  }

  binarySearch(element) {
    let minIndex = 0;
    let maxIndex = this.array.length - 1;
    let middleValue;
    while (minIndex <= maxIndex) {
      // 中间开始查找
      let middleIndex = parseInt((minIndex + maxIndex) / 2);
      middleValue = this.array[middleIndex];
      if (middleValue === element) {
        return middleIndex;
      } else if (middleValue > element) {
        // 左找
        // 中间位置的前一个开始
        maxIndex = middleIndex - 1;
      } else {
        // 中间位置的后一个开始
        minIndex = middleIndex + 1; // 右找
      }
    }
    return -1;
  }
}

let array = new ArrayList();
array.insert(1);
array.insert(2);
array.insert(3);
array.insert(4);
array.insert(5);
array.insert(19);
console.log(array.binarySearch(119));

数据结构&排序算法 ​

深度优先(DFS) ​

实现思路 ​

广度优先(BFS) ​

实现思路(利用栈的特性) ​

数组 ​

栈 ​

十进制转二进制 ​

队列 ​

普通队列 ​

优先级队列 ​

链表 ​

单向链表 ​

反转链表 ​

双向链表 ​

集合 ​

字典 ​

哈希表 ​

二叉树 ​

树的定义 ​

树的术语 ​

二叉树的特性 ​

冒泡排序 ​

选择排序 ​

插入排序 ​

希尔排序 ​

快速排序 ​

二分查找 ​

数据结构&排序算法

深度优先(DFS)

实现思路

广度优先(BFS)

实现思路(利用栈的特性)

数组

栈

十进制转二进制

队列

普通队列

优先级队列

链表

单向链表

反转链表

双向链表

集合

字典

哈希表

二叉树

树的定义

树的术语

二叉树的特性

冒泡排序

选择排序

插入排序

希尔排序

快速排序

二分查找